Acceleration Meaning
Acceleration is the vector that describes and quantifies changes in the speed of a moving object. Since speed is also a vector, its changes can be in magnitude, direction, and sense, or all at once.
This is a fundamental magnitude in Kinematics and is also part of many familiar situations: it is present when a car starts up when the traffic light turns green, it is present when a forward runs with the ball, and it can be experienced daily, like the turning feeling in the stomach when going up or down in an elevator.
Likewise, living beings are immersed in the Earth’s gravitational field, whose intensity is more or less constant (in reality it does experience some variations) and is known as g, the value of the Earth’s acceleration of gravity.
Acceleration is not synonymous with speed, although they are closely related. High acceleration does not necessarily imply that a vehicle is moving very fast. For example, a car can travel at 200 km/h on a straight highway, and have 0 acceleration, if its speed is not changing. And, on the contrary, a car can go very slowly, but have high acceleration, as when the car starts abruptly at a change in the traffic light or if it brakes suddenly.
Acceleration has units of speed over time. In the International System, speed is given in m/s, so acceleration is expressed in m/s 2 . For example, an acceleration of 4 m/s 2 means that for every second that passes, the object changes its speed by 4 m/s. Other combinations of units are also possible, such as km/h∙s or miles/h∙s. An acceleration of 0.5 km/h∙s is interpreted as follows: the object changes its speed by 0.5 km/h every second that passes.
Calculation of average acceleration
Acceleration can be expressed mathematically by its definition. Suppose that a moving object has an initial velocity called v o at time t o. Velocity is denoted in bold print or with an arrow above it, to differentiate it from a scalar quantity such as time, and it is always necessary to make the distinction since vectors have a very different nature than scalars.
If sometime later, at instant t f , the speed of the object in question becomes v f, since acceleration is the variation in speed during the time period in which such variation occurs, the average acceleration an m is defined as:
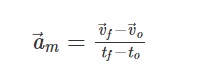
The difference between a final quantity and an initial quantity is denoted more compactly by the Greek letter Δ (read “delta”). Thanks to this notation, the average acceleration is also written as follows:
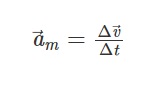
Instantaneous acceleration
The average acceleration, defined above, indicates the change in speed in a measurable instant of time Δt. But it would be better if the acceleration at each instant of the movement were known, so if that interval is made very, very small, we would have the instantaneous acceleration, that is, the acceleration at any instant.
Mathematically, making Δt very small means taking the limit of Δt as it tends to 0, without it actually reaching 0. With this in mind, the instantaneous acceleration or simply acceleration a of a moving object is:
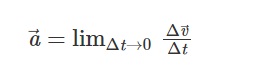
This limit is known as the derivative of velocity with respect to time. A derivative is the rate of change of a magnitude with respect to some variable, such as time, so:
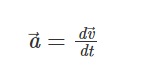
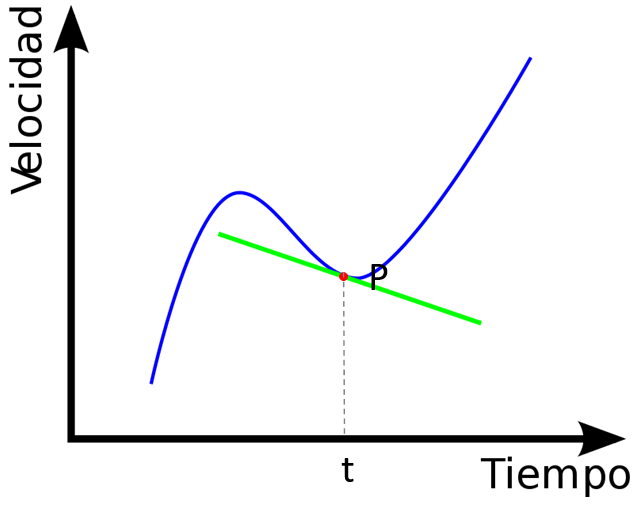
Geometrically, the derivative of a quantity with respect to a variable is interpreted as the slope of the tangent line to the curve that represents the quantity as a function of said variable, at a given point.
Representing the velocity function as a function of time on a graph, its derivative at point P corresponds to the slope of the line that passes through the point of tangency P in the following figure:
Another widely used notation for the derivative, apart from the one already shown, is the prime notation so that the acceleration can also be written as:
a = v´ (t)
Direction and sense of acceleration
The direction and sense of acceleration are as important as its magnitude or numerical value. The type of movement depends on it.
Acceleration can have the same direction as velocity or it can have any other direction. If the acceleration is non-zero and has the same direction as velocity, the direction of the latter does not change, but its magnitude does. The object may slow down or go faster and faster, depending on the direction of the acceleration.
To illustrate this fact, suppose a car is heading east at 90 km/h. If it has an acceleration that also points east, this means that the car is increasing the magnitude of its velocity (its speed), so the driver is pressing the accelerator pedal.
However, if the acceleration is directed towards the west, it means that the driver is stepping on the brakes and the speed of the vehicle is decreasing. To distinguish between both possibilities, signs are used, for example, towards the east it may be a + sign, and towards the west a − sign.
But in any case, the movement remains rectilinear, since the acceleration is not changing the direction of the speed in any way, only its magnitude. The movement thus described is known as uniformly varied rectilinear motion.
However, it is important to note that acceleration describes any change in velocity.
What happens if a moving object has constant acceleration, but in a direction perpendicular to its speed? The object would not experience a change in speed, which means that if it was moving at a rate of 90 km/h it would continue to maintain the same speed. But it would no longer be going in a straight line if it had been traveling in this way because this perpendicular acceleration forces it to follow a curved path.
And if before the object moved in a straight line, now it will do so with uniform circular motion (as long as the acceleration remains perpendicular to the speed and with constant magnitude).
In general, a car traveling on a road experiences a varied curvilinear motion, therefore, depending on the sections of the road, its acceleration can have components in various directions to adapt to the trajectory.
Acceleration Meaning in Hindi
त्वरण वह सदिश है जो किसी गतिशील वस्तु की गति में होने वाले परिवर्तनों का वर्णन और परिमाणन करता है। चूँकि गति भी एक सदिश है, इसलिए इसके परिवर्तन परिमाण, दिशा और अर्थ में या एक साथ हो सकते हैं।
यह गतिविज्ञान में एक मौलिक परिमाण है और कई परिचित स्थितियों का भी हिस्सा है: यह तब मौजूद होता है जब ट्रैफ़िक लाइट हरी होने पर कार स्टार्ट होती है, यह तब मौजूद होता है जब कोई फ़ॉरवर्ड गेंद के साथ दौड़ता है, और इसे रोज़ाना अनुभव किया जा सकता है, जैसे लिफ्ट में ऊपर या नीचे जाते समय पेट में होने वाली घबराहट।
इसी तरह, जीवित प्राणी पृथ्वी के गुरुत्वाकर्षण क्षेत्र में डूबे रहते हैं, जिसकी तीव्रता कमोबेश स्थिर होती है (वास्तव में यह कुछ बदलावों का अनुभव करता है) और इसे g के रूप में जाना जाता है, जो पृथ्वी के गुरुत्वाकर्षण के त्वरण का मान है।
त्वरण गति का पर्याय नहीं है, हालाँकि वे निकट से संबंधित हैं। उच्च त्वरण का अर्थ यह नहीं है कि कोई वाहन बहुत तेज़ गति से चल रहा है। उदाहरण के लिए, एक कार सीधे राजमार्ग पर 200 किमी/घंटा की गति से यात्रा कर सकती है, और यदि इसकी गति नहीं बदल रही है, तो इसका त्वरण 0 हो सकता है। और, इसके विपरीत, एक कार बहुत धीमी गति से चल सकती है, लेकिन उसमें उच्च त्वरण हो सकता है, जैसे कि जब कार ट्रैफ़िक लाइट में बदलाव पर अचानक शुरू होती है या अगर यह अचानक ब्रेक लगाती है। ##
त्वरण में समय के साथ गति की इकाइयाँ होती हैं। अंतर्राष्ट्रीय प्रणाली में, गति m/s में दी जाती है, इसलिए त्वरण m/s 2 में व्यक्त किया जाता है। उदाहरण के लिए, 4 m/s 2 के त्वरण का अर्थ है कि हर सेकंड के लिए, वस्तु अपनी गति 4 m/s से बदलती है। इकाइयों के अन्य संयोजन भी संभव हैं, जैसे कि km/h∙s या miles/h∙s। 0.5 km/h∙s के त्वरण की व्याख्या इस प्रकार की जाती है: वस्तु अपनी गति को हर सेकंड के लिए 0.5 km/h से बदलती है। ##
औसत त्वरण की गणना
त्वरण को गणितीय रूप से इसकी परिभाषा द्वारा व्यक्त किया जा सकता है। मान लीजिए कि एक चलती वस्तु का समय t o पर प्रारंभिक वेग v o है। वेग को समय जैसी अदिश राशि से अलग करने के लिए मोटे अक्षरों में या उसके ऊपर तीर से दर्शाया जाता है, और यह अंतर करना हमेशा आवश्यक होता है क्योंकि सदिशों की प्रकृति अदिश राशियों से बहुत अलग होती है।
यदि कुछ समय बाद, क्षण t f पर, विचाराधीन वस्तु की गति v f हो जाती है, क्योंकि त्वरण उस समय अवधि के दौरान गति में परिवर्तन है जिसमें ऐसा परिवर्तन होता है, तो औसत त्वरण an m को इस प्रकार परिभाषित किया जाता है:
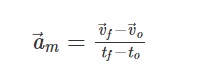
अंतिम मात्रा और प्रारंभिक मात्रा के बीच के अंतर को ग्रीक अक्षर Δ (पढ़ें “डेल्टा”) द्वारा अधिक स्पष्ट रूप से दर्शाया जाता है। इस संकेतन के कारण, औसत त्वरण भी इस प्रकार लिखा जाता है:
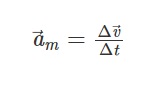
तात्कालिक त्वरण
ऊपर परिभाषित औसत त्वरण, समय के एक मापनीय क्षण Δt में गति में परिवर्तन को इंगित करता है। लेकिन यह बेहतर होगा यदि गति के प्रत्येक क्षण पर त्वरण ज्ञात हो, इसलिए यदि उस अंतराल को बहुत, बहुत छोटा कर दिया जाए, तो हमें तात्कालिक त्वरण मिलेगा, अर्थात किसी भी क्षण पर त्वरण।
गणितीय रूप से, Δt को बहुत छोटा बनाने का मतलब है Δt की सीमा को 0 की ओर ले जाना, बिना वास्तव में 0 तक पहुँचे। इसे ध्यान में रखते हुए, किसी गतिशील वस्तु का तात्कालिक त्वरण या बस त्वरण a है:
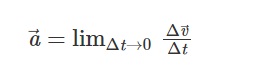
इस सीमा को समय के संबंध में वेग का व्युत्पन्न कहा जाता है। व्युत्पन्न किसी चर, जैसे समय, के संबंध में परिमाण के परिवर्तन की दर है, इसलिए:
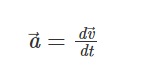
ज्यामितीय रूप से, किसी चर के संबंध में किसी मात्रा के व्युत्पन्न को उस वक्र की स्पर्शरेखा रेखा के ढलान के रूप में व्याख्या किया जाता है जो किसी दिए गए बिंदु पर उक्त चर के फ़ंक्शन के रूप में मात्रा का प्रतिनिधित्व करता है।
वेग फ़ंक्शन को ग्राफ़ पर समय के फ़ंक्शन के रूप में दर्शाते हुए, बिंदु P पर इसका व्युत्पन्न उस रेखा के ढलान के अनुरूप है जो निम्न चित्र में स्पर्शरेखा बिंदु P से होकर गुजरती है:

व्युत्पन्न के लिए एक और व्यापक रूप से इस्तेमाल किया जाने वाला संकेतन, पहले से दिखाए गए के अलावा, प्राइम नोटेशन है ताकि त्वरण को इस प्रकार भी लिखा जा सके:
a = v´ (t)
त्वरण की दिशा और भावना
त्वरण की दिशा और भावना उतनी ही महत्वपूर्ण है जितनी कि इसका परिमाण या संख्यात्मक मान। गति का प्रकार इस पर निर्भर करता है।
त्वरण की दिशा वेग के समान हो सकती है या इसकी कोई अन्य दिशा भी हो सकती है। यदि त्वरण शून्य नहीं है और इसकी दिशा वेग के समान है, तो उत्तरार्द्ध की दिशा नहीं बदलती है, लेकिन इसका परिमाण बदल जाता है। त्वरण की दिशा के आधार पर वस्तु धीमी हो सकती है या तेज़ और तेज़ हो सकती है।
इस तथ्य को स्पष्ट करने के लिए, मान लीजिए कि एक कार 90 किमी/घंटा की गति से पूर्व की ओर जा रही है। यदि इसका त्वरण भी पूर्व की ओर है, तो इसका मतलब है कि कार अपने वेग (अपनी गति) के परिमाण को बढ़ा रही है, इसलिए चालक एक्सीलेटर पेडल दबा रहा है।
हालाँकि, यदि त्वरण पश्चिम की ओर निर्देशित है, तो इसका मतलब है कि चालक ब्रेक पर कदम रख रहा है और वाहन की गति कम हो रही है। दोनों संभावनाओं के बीच अंतर करने के लिए, संकेतों का उपयोग किया जाता है, उदाहरण के लिए, पूर्व की ओर यह + चिह्न हो सकता है, और पश्चिम की ओर − चिह्न हो सकता है।
लेकिन किसी भी मामले में, गति सीधी रेखा में रहती है, क्योंकि त्वरण किसी भी तरह से गति की दिशा नहीं बदल रहा है, केवल इसका परिमाण बदल रहा है। इस प्रकार वर्णित गति को समान रूप से भिन्न रेखीय गति के रूप में जाना जाता है।
हालांकि, यह ध्यान रखना महत्वपूर्ण है कि त्वरण वेग में किसी भी परिवर्तन का वर्णन करता है।
क्या होता है यदि किसी गतिशील वस्तु में निरंतर त्वरण होता है, लेकिन उसकी गति के लंबवत दिशा में? वस्तु की गति में कोई परिवर्तन नहीं होगा, जिसका अर्थ है कि यदि वह 90 किमी/घंटा की दर से आगे बढ़ रही थी, तो वह उसी गति को बनाए रखेगी। लेकिन यदि वह इस तरह से यात्रा कर रही होती तो वह अब सीधी रेखा में नहीं जा रही होती क्योंकि यह लंबवत त्वरण उसे एक घुमावदार पथ का अनुसरण करने के लिए मजबूर करता है।
और यदि पहले वस्तु सीधी रेखा में चलती थी, तो अब वह एकसमान वृत्ताकार गति के साथ ऐसा करेगी (जब तक त्वरण गति के लंबवत और स्थिर परिमाण के साथ रहता है)।
सामान्य तौर पर, सड़क पर यात्रा करने वाली कार एक विविध वक्रीय गति का अनुभव करती है, इसलिए, सड़क के खंडों के आधार पर, इसके त्वरण में प्रक्षेप पथ के अनुकूल होने के लिए विभिन्न दिशाओं में घटक हो सकते हैं।
